Learning a Decision Tree (classification)
Decision Tree
Sharif University Of technology - Computer Engineering Depatment
Artifical Intelligence - Dr. MH Rohban
Spring 2021
Spring 2021
Decision Tree And Its Application In Classification
Writers Team
Amirsadra Abdollahi
Ashkan Khademian
Amirmohammad Isazadeh
What's Decision Tree
Decision tree learning is a method commonly used in data mining. The goal is to create a model that predicts the value of a target variable based on several input variables.
A decision tree is a simple representation for classifying examples. For this section, assume that all of the input features have finite discrete domains, and there is a single target feature called the "classification". Each element of the domain of the classification is called a class. A decision tree or a classification tree is a tree in which each internal (non-leaf) node is labeled with an input feature. The arcs coming from a node labeled with an input feature are labeled with each of the possible values of the target feature or the arc leads to a subordinate decision node on a different input feature. Each leaf of the tree is labeled with a class or a probability distribution over the classes, signifying that the data set has been classified by the tree into either a specific class, or into a particular probability distribution(which,if the decision tree is well-constructed, is skewed towards certain subsets of classes).
Overview
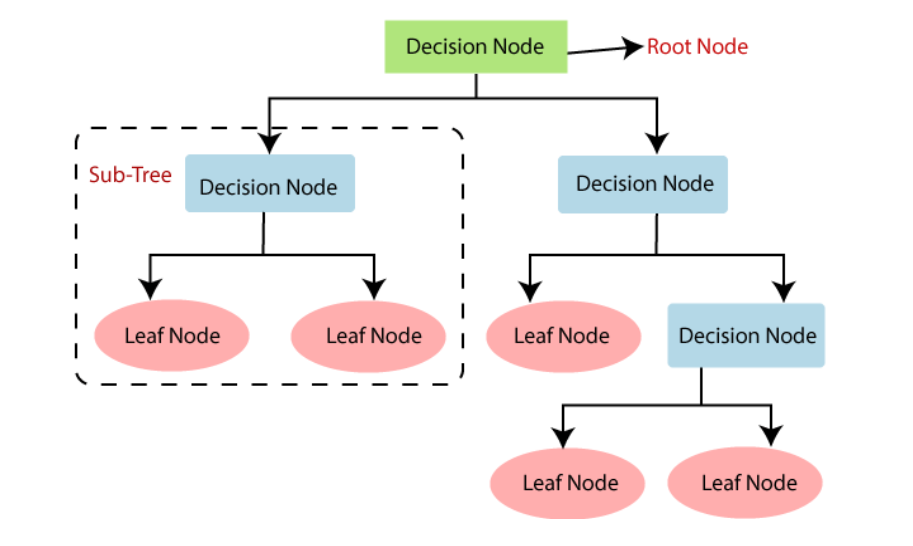
Decision Tree Examples
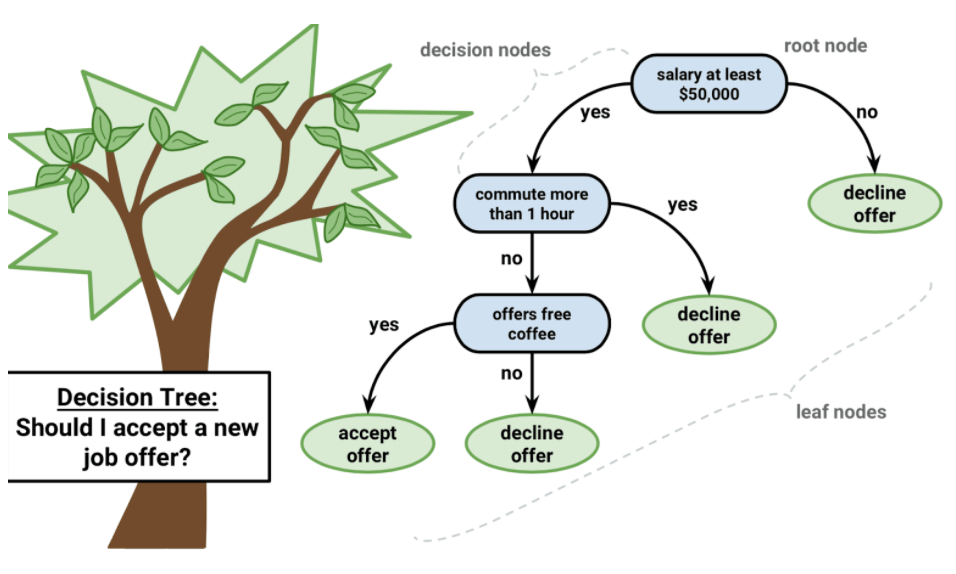
1. Accept A New Job Offer
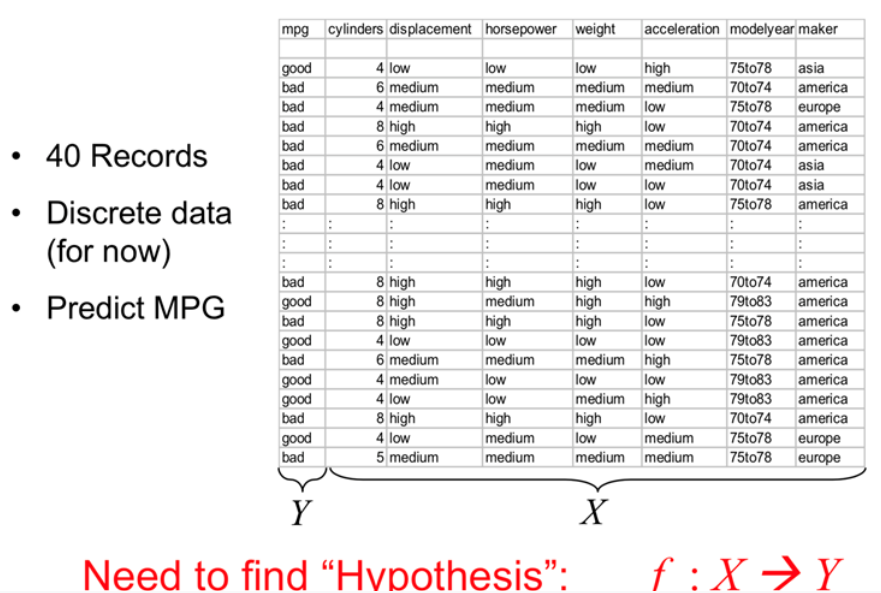
2. Predict Fuel Efficiency
1. Accept A New Job Offer

2. Predict Fuel Efficiency

Building A Decision Tree
Now we want to build a decision tree for Fuel Efficiency Example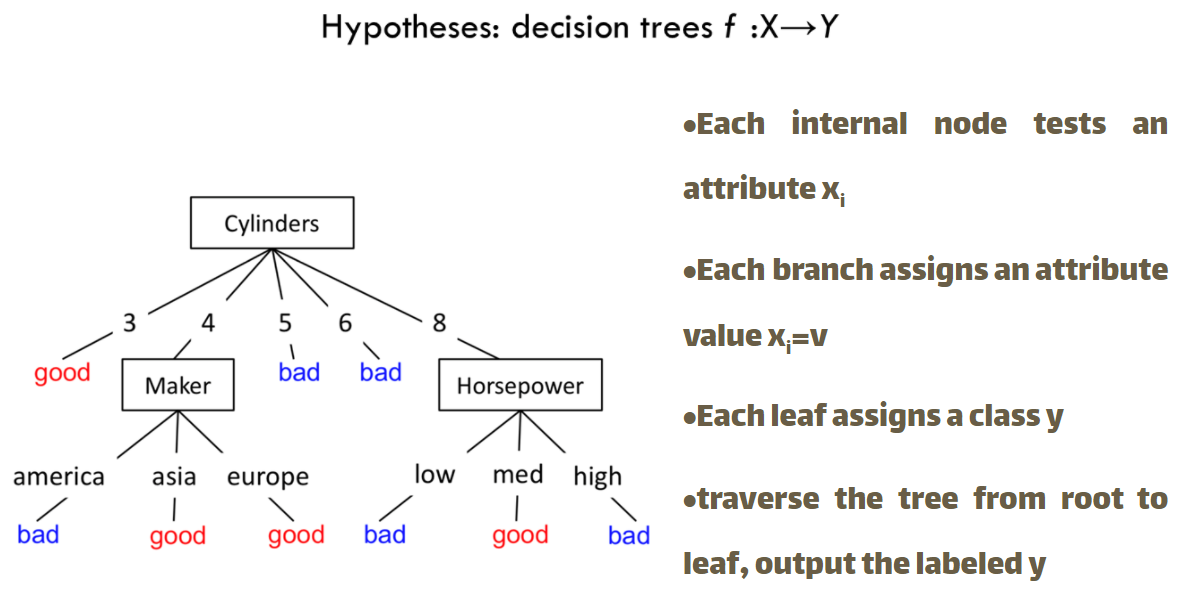

Now we want to build a decision tree for Fuel Efficiency Example

Build decision Tree
The Starting Node
We can start with an empty tree and improve it at each level. For example, for the second example we have a tree that for all data, it returns mpg=bad. So for our dataset we got 22 correct answers and 18 wrong answers with this tree. but we can improve it!
</div>
Operators
There are several operators for building a decision tree.Improving the tree
To improve our tree, we can add more nodes(features) to get more correct answer and predict better.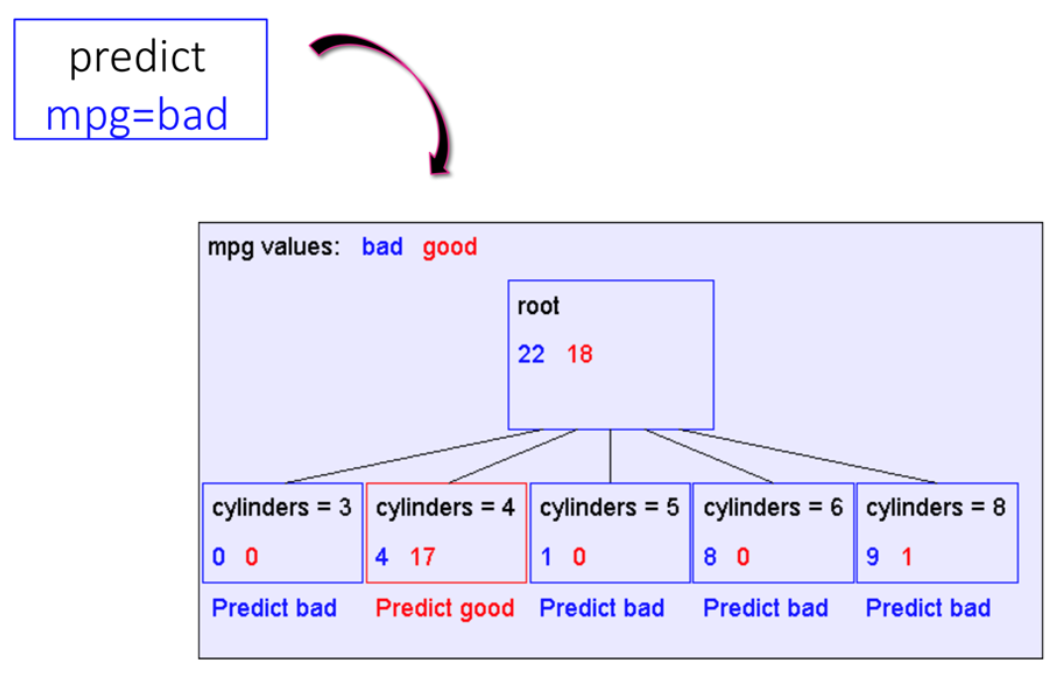
Recursive step
We can consider each leaf as a root and do the same for those.Maybe we get to some node that doesn’t have any data. In these situations we should end up and predict randomly.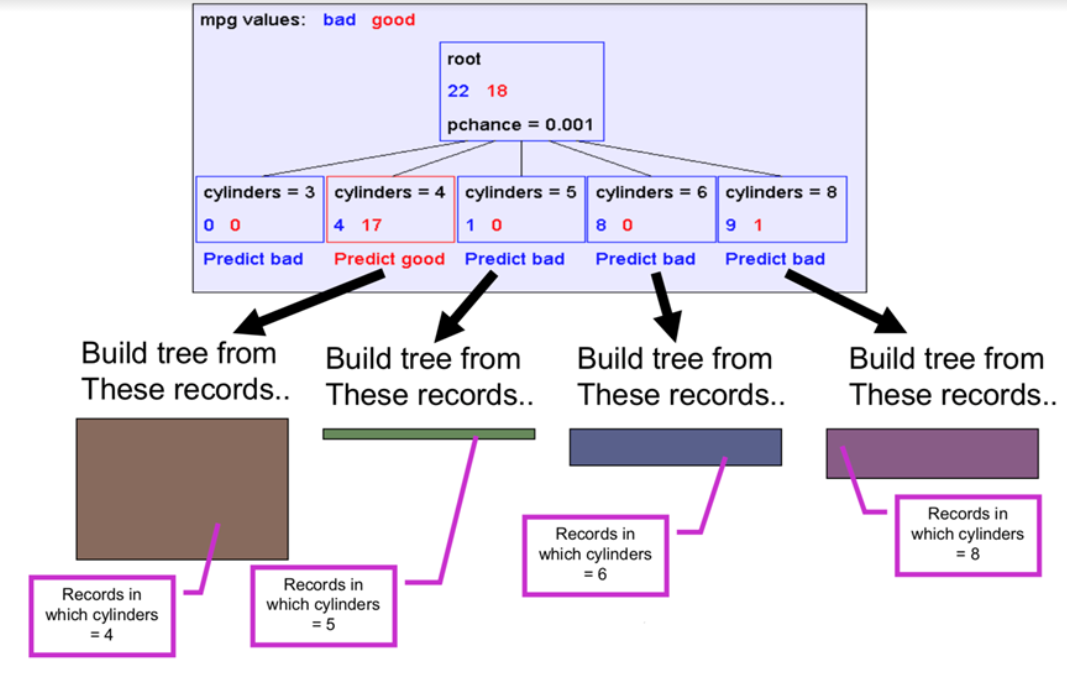 After one level we got this tree ?
After one level we got this tree ?
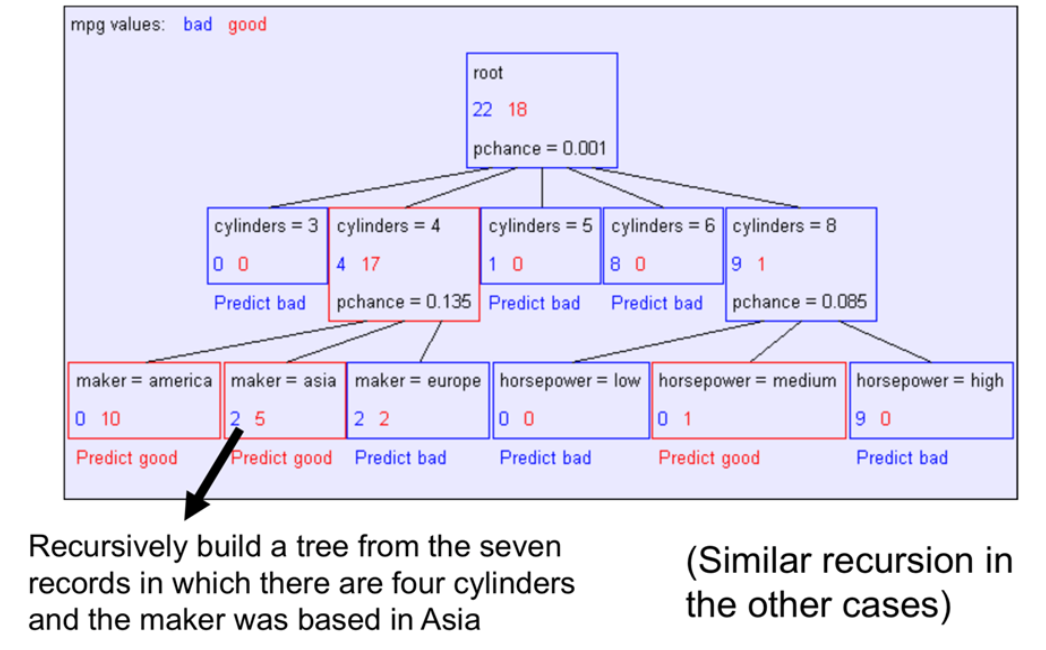 And after adding all nodes(features) to the tree we got a Full Tree like this:
And after adding all nodes(features) to the tree we got a Full Tree like this:
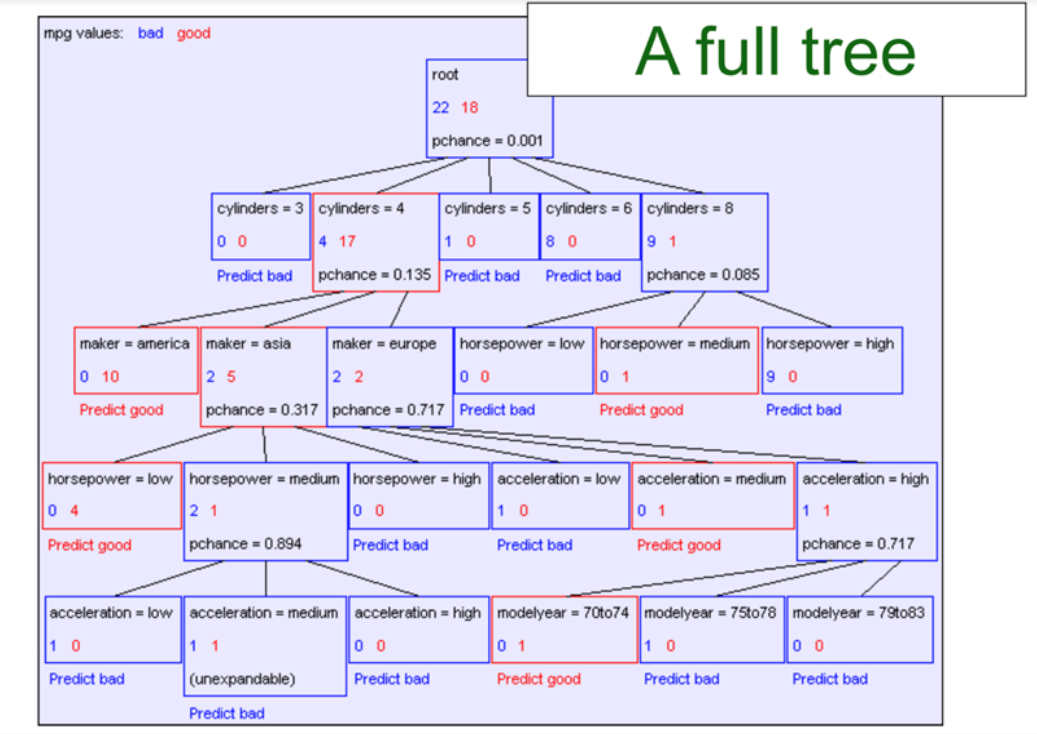
Two Questions For More Efficiency
Hill Climbing Algorithm:
•Start from empty decision tree •Split on the best attribute (feature) – Recurse Now the important question is: •Which attribute gives the best split? •When to stop recursion?Splitting: choosing a good attribute
Look at the example to get the main point of splitting!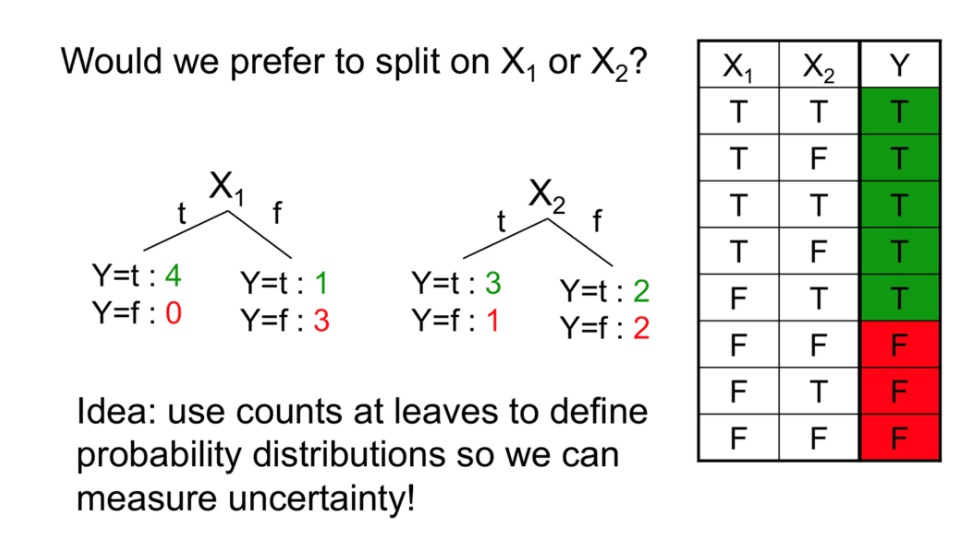
Measuring uncertainty
•Good split if we are more certain about classification after split
•Deterministic good (all true or all false)
•Uniform distribution? BAD
Which attribute gives the best split?
• A1: The one with the highest information gain• Defined in terms of entropy
• A2: Actually many alternatives,
• e.g., accuracy. Seeks to reduce the misclassification rate
Entropy And Information Gain
Entropy
First we start with definition of entropy:
Entropy H(Y) of a random variable Y: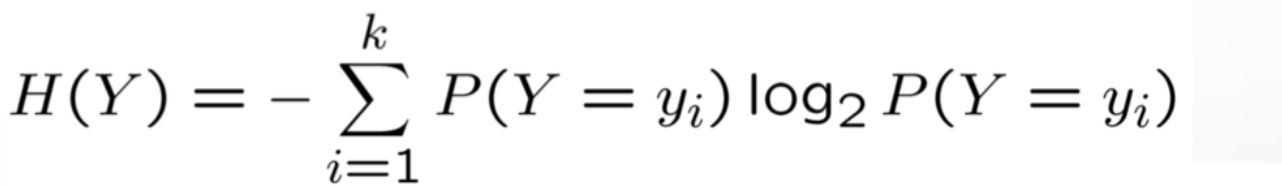 As it can be figured out, more uncertainty, more entropy!
As it can be figured out, more uncertainty, more entropy!
It's interesting to know that in Information Theory interpretation entropy is defined as:
Expected number of bits needed to encode a randomly drawn value of Y (under most efficient code)
And for a diagram view of entropy we can say it has a peak in the middle of it, then it falls.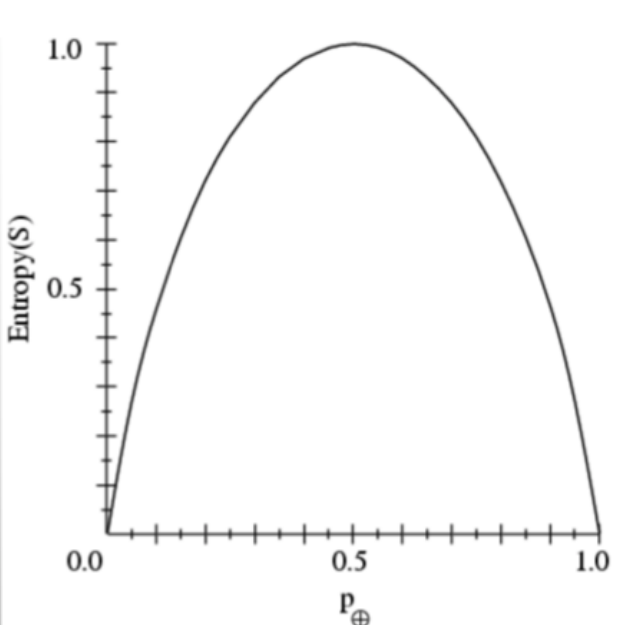 Example of Entropy
Example of Entropy
If P(Y=t) = 5/6 and P(Y=f) = 1/6 the value of H(Y) would be: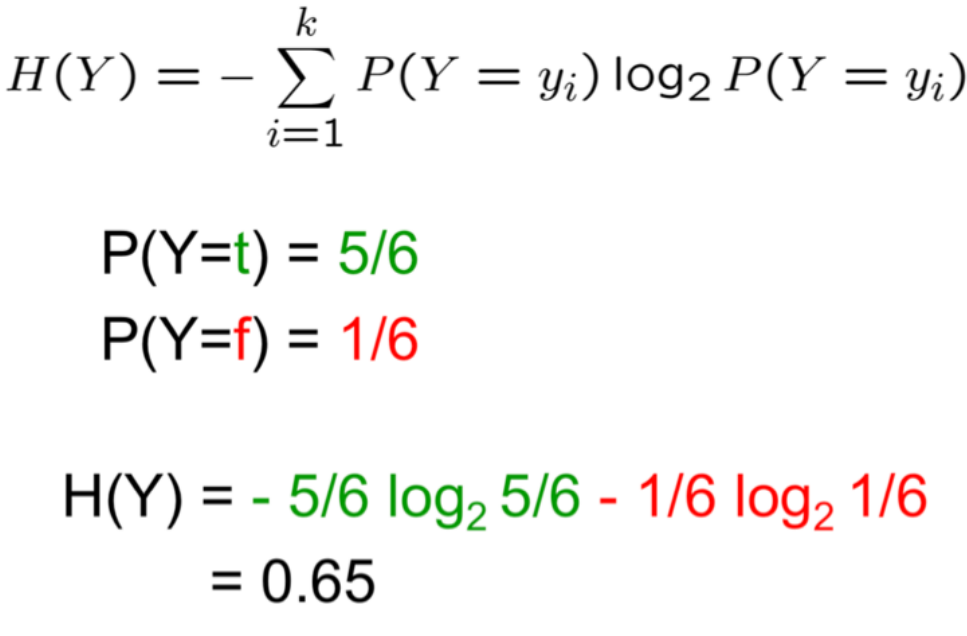 Conditional Entropy
Conditional Entropy
definition:
Conditional Entropy H(Y|X) of a random variable Y conditioned on a random variable X
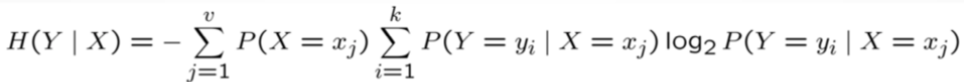 And here an example of conditional entropy:
And here an example of conditional entropy:
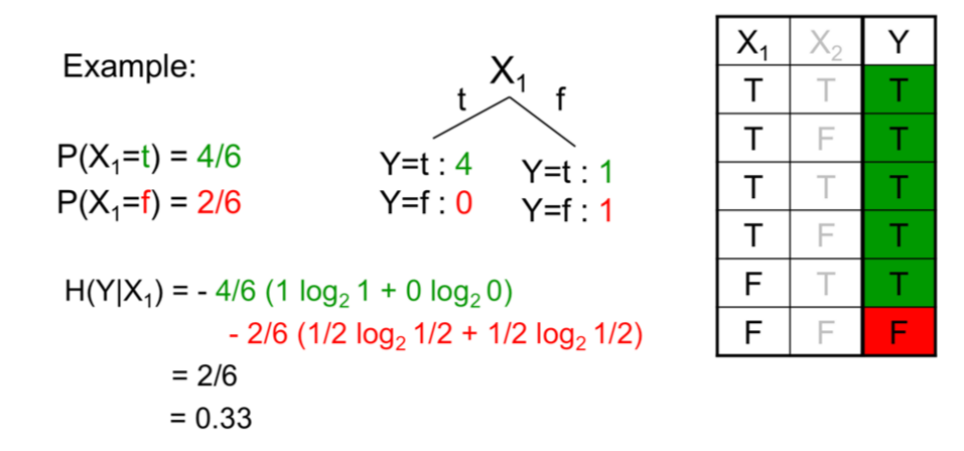
Entropy
First we start with definition of entropy:
Entropy H(Y) of a random variable Y:
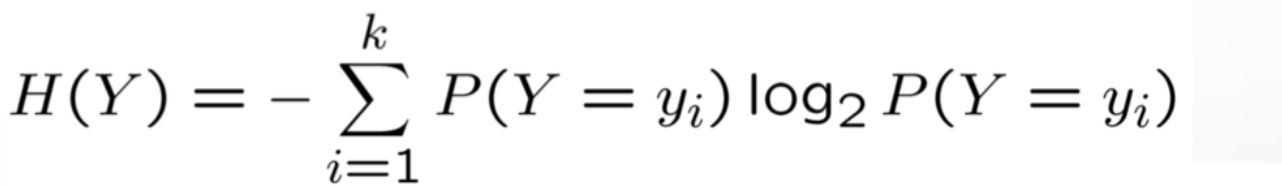 As it can be figured out, more uncertainty, more entropy!
As it can be figured out, more uncertainty, more entropy!It's interesting to know that in Information Theory interpretation entropy is defined as:
Expected number of bits needed to encode a randomly drawn value of Y (under most efficient code)
And for a diagram view of entropy we can say it has a peak in the middle of it, then it falls.
 Example of Entropy
Example of EntropyIf P(Y=t) = 5/6 and P(Y=f) = 1/6 the value of H(Y) would be:
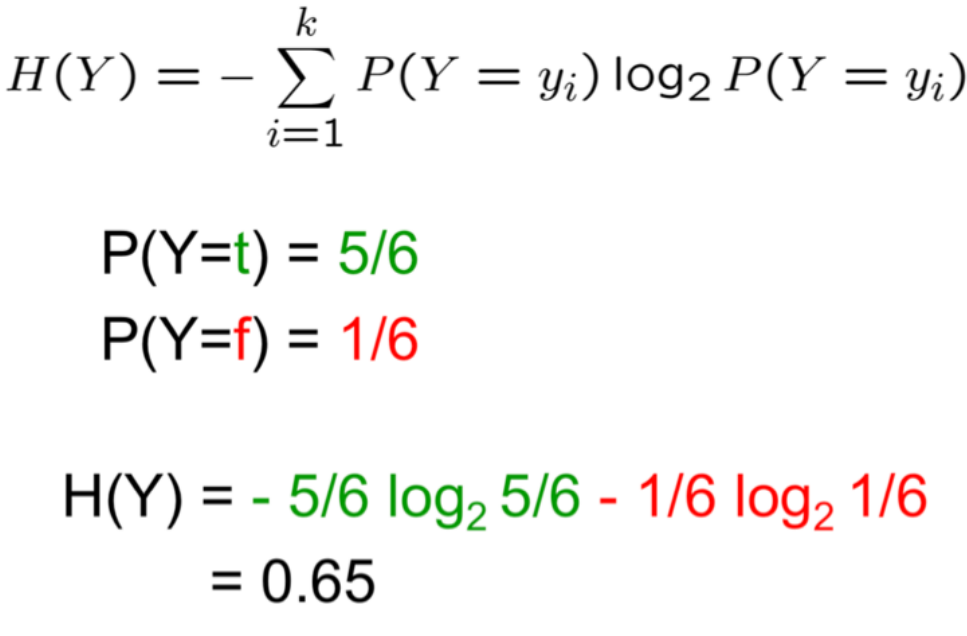 Conditional Entropy
Conditional Entropydefinition:
Conditional Entropy H(Y|X) of a random variable Y conditioned on a random variable X
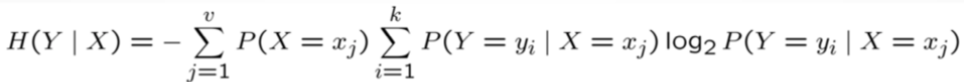 And here an example of conditional entropy:
And here an example of conditional entropy:
Information Gain
definition:
The information gain is the amount of information gained about a random variable or signal from observing another random variable and defined by this equation: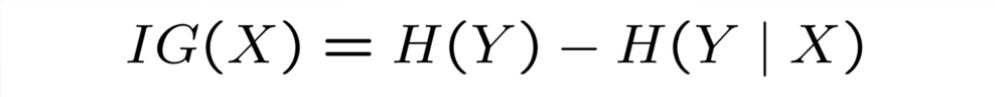 And for IG of our last example we have:
And for IG of our last example we have:

definition:
The information gain is the amount of information gained about a random variable or signal from observing another random variable and defined by this equation:
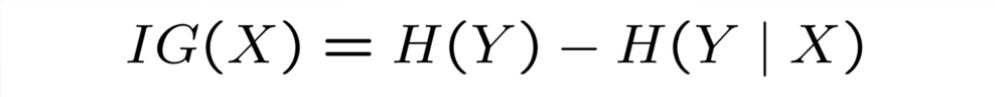 And for IG of our last example we have:
And for IG of our last example we have:

Learning Decision Tree
For learning a decision tree we should consider some important things such as:
. Select a node for splitting
. Update tree after an iteration
. Terminating condition
Steps of building a tree:
. Start from empty decision tree
. Split on next best attribute (feature)
. Use information gain (or...?) to select attribute:
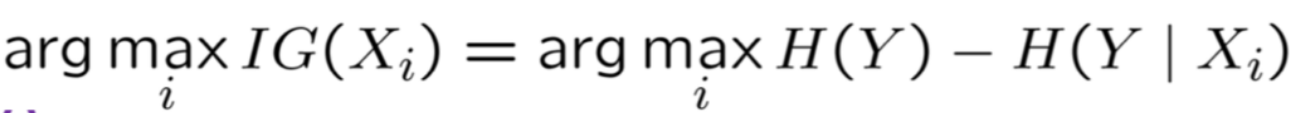 . Recurse
. Recurse
Example
Now we want to build a tree step by step, as an example for figuring out the way to build a DT.
Suppose we want to predict MPG; now look at all the information gains in the picture below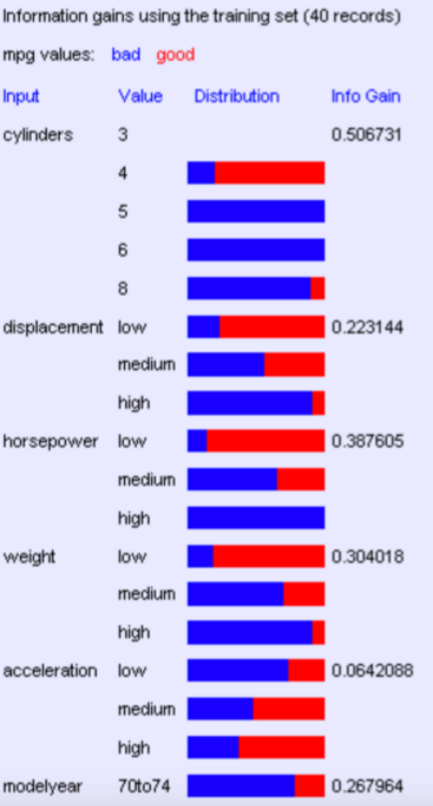 Now we should do our iterations.
Now we should do our iterations.
For first iteration we have: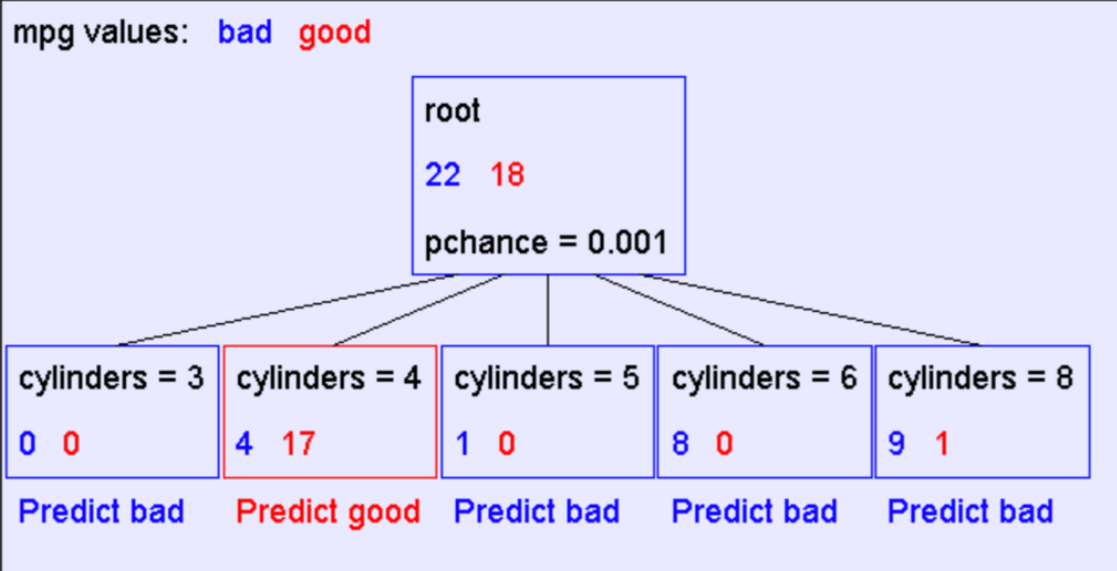
For learning a decision tree we should consider some important things such as:
. Select a node for splitting
. Update tree after an iteration
. Terminating condition
Steps of building a tree:
. Start from empty decision tree
. Split on next best attribute (feature)
. Use information gain (or...?) to select attribute:
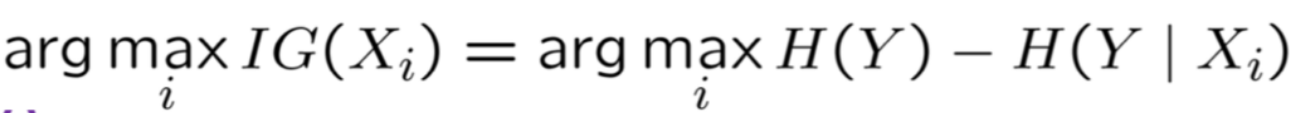 . Recurse
. RecurseExample
Now we want to build a tree step by step, as an example for figuring out the way to build a DT.
Suppose we want to predict MPG; now look at all the information gains in the picture below
 Now we should do our iterations.
Now we should do our iterations.For first iteration we have:

Termination Conditions
We introduce conditions to know when to stop building process.
Two ideas for terminating are:
. Base Case One: If all records in current data subset have the same output then don’t recurse.
. Base Case Two: If all records have exactly the same set of input attributes then don’t recurse.
Base Case One: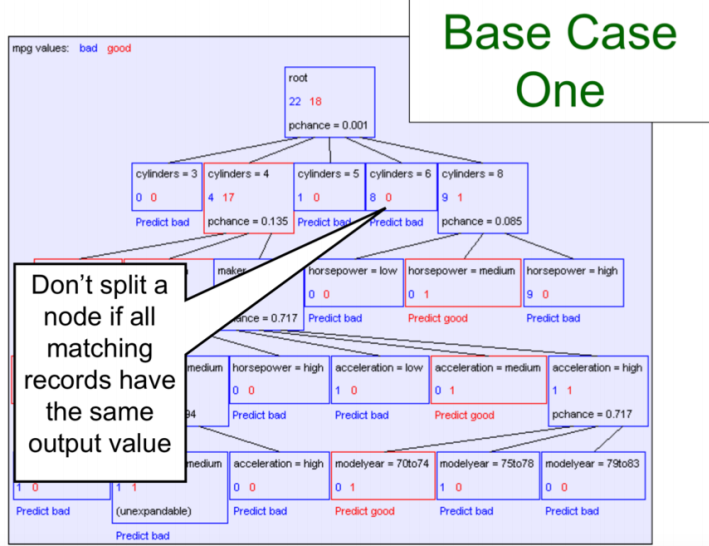 Base Case Two:
Base Case Two:
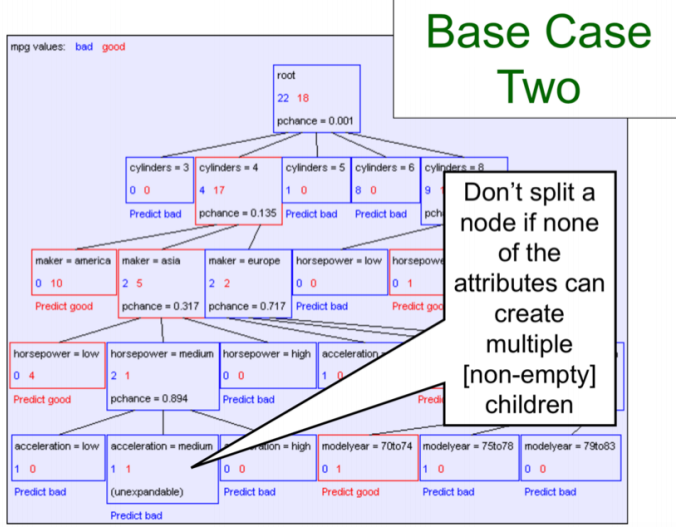
Now there is one other idea for termination that we want to discuss:
. Base Case 3: If all attributes have zero information gain then don't recurse.
Is it a good idea??
The answer is no!!
Because it's kind of a greedy idea!!
In this idea we check information gain of our variables alone, but if we check the information we get from combination of variables, there maybe be usefull information.
Here an example of this idea's problem:
For Y = a xor b, we use this idea and here the result: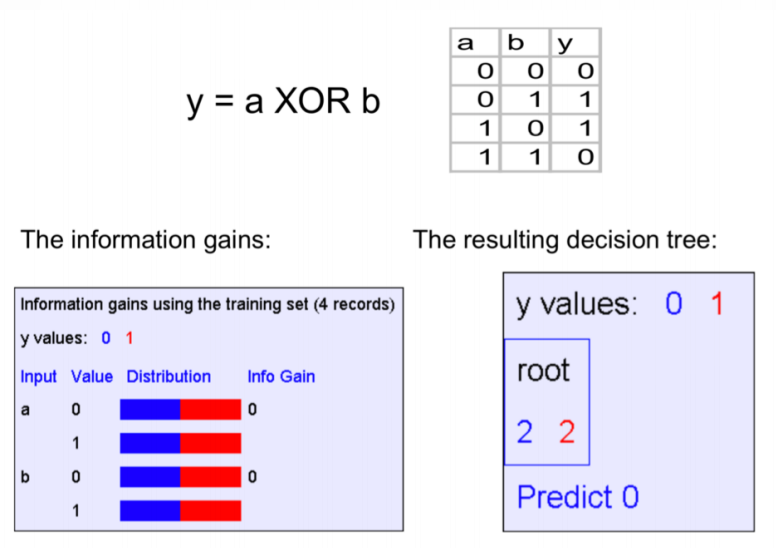 But without this idea:
But without this idea:
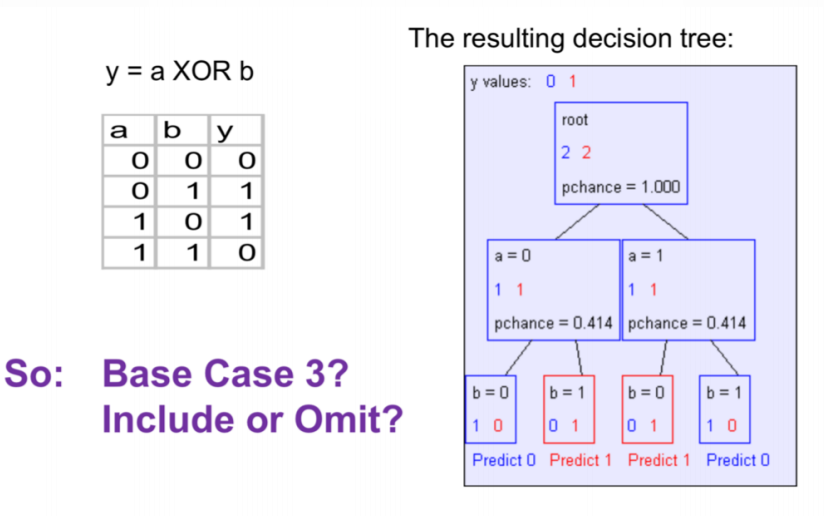

 So as we can see, this idea didn't come up with good results.
So as we can see, this idea didn't come up with good results.
We introduce conditions to know when to stop building process.
Two ideas for terminating are:
. Base Case One: If all records in current data subset have the same output then don’t recurse.
. Base Case Two: If all records have exactly the same set of input attributes then don’t recurse.
Base Case One:
 Base Case Two:
Base Case Two:

Now there is one other idea for termination that we want to discuss:
. Base Case 3: If all attributes have zero information gain then don't recurse.
Is it a good idea??
The answer is no!!
Because it's kind of a greedy idea!!
In this idea we check information gain of our variables alone, but if we check the information we get from combination of variables, there maybe be usefull information.
Here an example of this idea's problem:
For Y = a xor b, we use this idea and here the result:
 But without this idea:
But without this idea:


 So as we can see, this idea didn't come up with good results.
So as we can see, this idea didn't come up with good results.
Overfitting in Decision Trees
How to resolve Overfitting ?
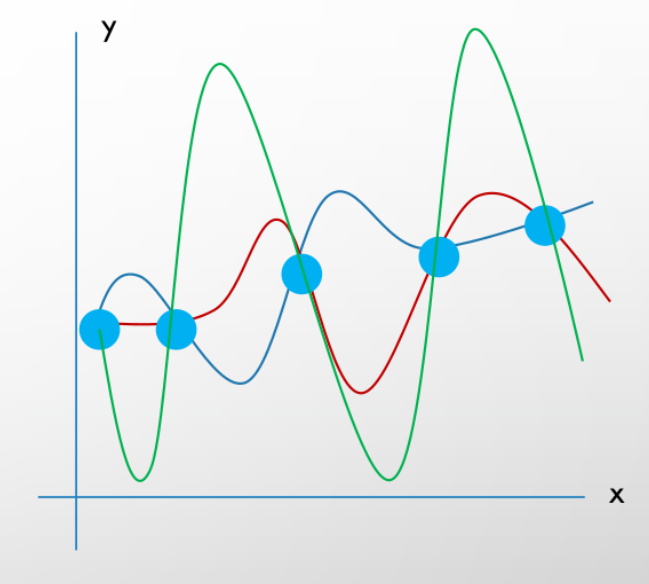
Decision trees have no learning bias and in outcome, the variance over the training set is significantly high. How can we introduce some biases to resolve the overfitting?No Free Lunch Theorem
Take the facing graph as an example. Suppose we are given a dataset of (x, y)s and we want to estimate the function which caused these points. As you might’ve gotten it so far, all the three functions (red, green, and blue) are estimating it right and if we don’t have any prior knowledge, all three functions have the exact probability to be our suggesting function. “No Free lunch” states that, in absence of any sense on what functions are more likely, learning is impossible. For example, if we already knew that a very smooth function generated these points we are more likely to prefer the blue function to others.
Occam’s Razor :
This principle states that from all possible hypotheses on a dataset, choose the shortest (the least complex) one. Because a short hypothesis is less likely to overfit.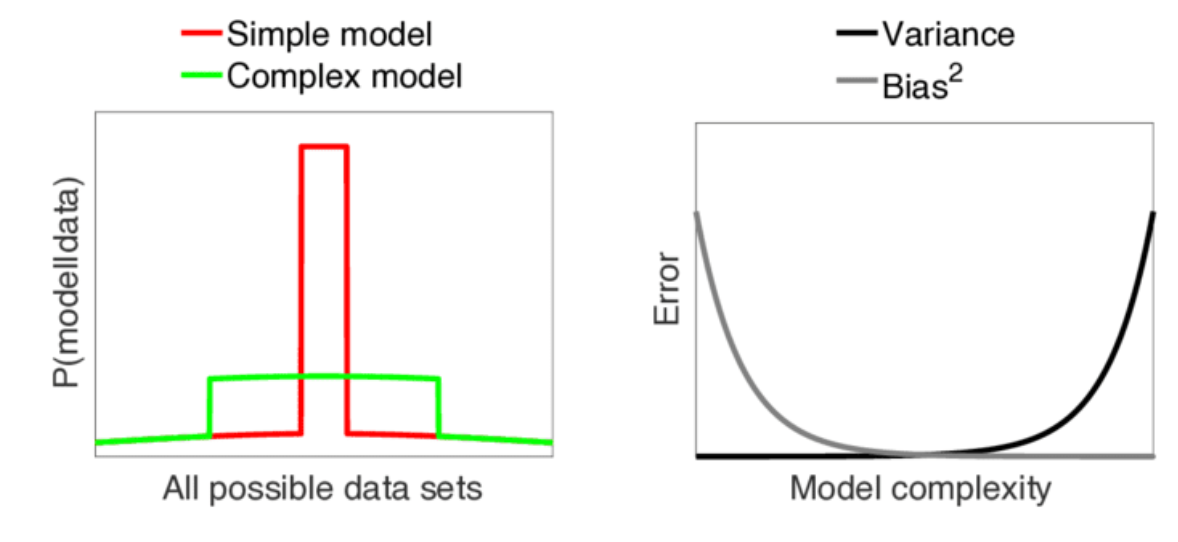
According to this principle we’d rather make smaller trees with less depth.
This principle states that from all possible hypotheses on a dataset, choose the shortest (the least complex) one. Because a short hypothesis is less likely to overfit.

Variance of model
If we change the training data, how much our result on validation set changesBias of model
The deviation we took from the original training data while we were trainingAccording to this principle we’d rather make smaller trees with less depth.
How To Build Small Trees
There are some approaches as followed:
Stop growing tree before overfit
. Bound depth or #leaves
. Stop growing more depth if in one depth Information Gain (IG) of all
. features on remaining data is zero.
Grow full tree then prune
. Optimize on a held-out (validation set). Meaning after the training is finished prune any branches that do not reduce the accuracy on validation set below a threshold. (Con: requires a larger amount of data)
. Use statistical significance testing
There are some approaches as followed:
Stop growing tree before overfit
. Bound depth or #leaves
. Stop growing more depth if in one depth Information Gain (IG) of all
. features on remaining data is zero.
Grow full tree then prune
. Optimize on a held-out (validation set). Meaning after the training is finished prune any branches that do not reduce the accuracy on validation set below a threshold. (Con: requires a larger amount of data)
. Use statistical significance testing
Use statistical significance testing
Chi-Square Test (remembrance)
Having two features where the first feature has k classes and the second one has n classes. With people which we know their classes in both features, H0(null hypothesis) states that in a table with k rows and n columns, rows are independent from columns and conversely.
 Using Chi-Square in growing tree
Using Chi-Square in growing tree
As you know, for choosing what feature to be used in each depth we got help from a concept called IG. after the tree is grown (fully or with a limit on depth and leaves) we test each feature in each depth and calculate the p_value. After setting a threshold calledMaxPchance, if calculate pfor any feature is greater than MaxPchance. We prune that feature and the decision will be based on the previous feature (parent node). How to find a good MaxPchance? We could use a local or greedy search on the validation set and by reaching a good accuracy on the validation set we would stop and set that MaxPchance.
Having two features where the first feature has k classes and the second one has n classes. With people which we know their classes in both features, H0(null hypothesis) states that in a table with k rows and n columns, rows are independent from columns and conversely.
 Using Chi-Square in growing tree
Using Chi-Square in growing treeAs you know, for choosing what feature to be used in each depth we got help from a concept called IG. after the tree is grown (fully or with a limit on depth and leaves) we test each feature in each depth and calculate the p_value. After setting a threshold calledMaxPchance, if calculate pfor any feature is greater than MaxPchance. We prune that feature and the decision will be based on the previous feature (parent node). How to find a good MaxPchance? We could use a local or greedy search on the validation set and by reaching a good accuracy on the validation set we would stop and set that MaxPchance.
Additional Content
Random Forests
Idea:
Decision Trees overfit easily and it's hard to grow them on a big number of features.
Approach:
Use multiple decision trees instead of only one.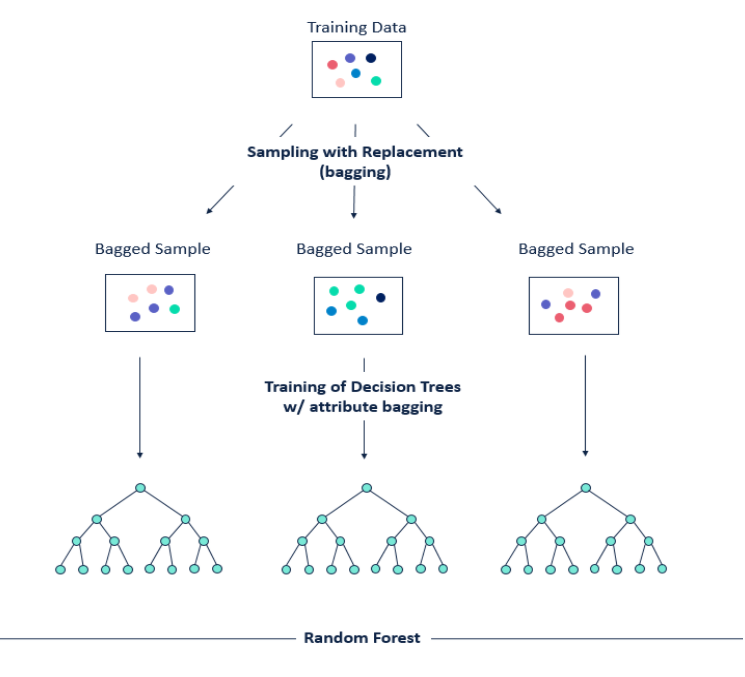 For each tree:
For each tree:
Training Set
Assume T as the original training set. It’s not usual to divide it into N subsets (N number of decision trees in forest). For the sake of resolving the overfit, we choose a subset size of $φ1|T|$ then we bootstrap (bagging) T into N subsets of size $φ1|T|$. ($0 < φ1|T| <=1$)
Features
One Problem of a single decision tree was that it was hard to grow it on a lot of features. Then here we choose randomly a subset of features with size $φ2|F|$ and assign it to each tree in the forest. ($0 < φ2|F| <=1$)
Prediction
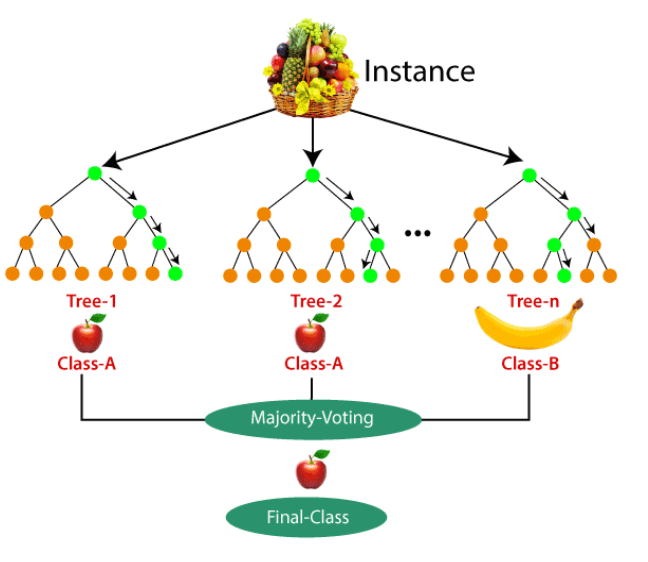
There are two methods to report the final prediction of each sample of the test set.
1. Max Method
In this method we report the class which is predicted the most. for example if 3 out of 5 trees said the class is 𝑌=1 we report 𝑌=1 . properties:
. less F1 score
. more recall
. less precision
. should choose randomly when the number of trees is even
2. Avg Method
As we know each tree has a probability with its prediction which shows how much does he persist that its answer is true. We calculate a weighted average of each tree's prediction where the weights are the probability reported from each tree alongside its prediction.
properties:
. more F1
. less recall
. more precision
. has a more reasonable answer when the number of trees is even
Random Forests
Idea:
Decision Trees overfit easily and it's hard to grow them on a big number of features.
Approach:
Use multiple decision trees instead of only one.
 For each tree:
For each tree:Training Set
Assume T as the original training set. It’s not usual to divide it into N subsets (N number of decision trees in forest). For the sake of resolving the overfit, we choose a subset size of $φ1|T|$ then we bootstrap (bagging) T into N subsets of size $φ1|T|$. ($0 < φ1|T| <=1$)
Features
One Problem of a single decision tree was that it was hard to grow it on a lot of features. Then here we choose randomly a subset of features with size $φ2|F|$ and assign it to each tree in the forest. ($0 < φ2|F| <=1$)
Prediction
There are two methods to report the final prediction of each sample of the test set.
1. Max Method
In this method we report the class which is predicted the most. for example if 3 out of 5 trees said the class is 𝑌=1 we report 𝑌=1 . properties:
. less F1 score
. more recall
. less precision
. should choose randomly when the number of trees is even
2. Avg Method
As we know each tree has a probability with its prediction which shows how much does he persist that its answer is true. We calculate a weighted average of each tree's prediction where the weights are the probability reported from each tree alongside its prediction.
properties:
. more F1
. less recall
. more precision
. has a more reasonable answer when the number of trees is even



