Bayesian Networks Representation
Bayesian Network: Representation¶
Table of Content¶
D-separation¶
In this section we're going to present a procedure named D-separation which determines different kinds of conditional independences without algebraic operations.
### Outline To get to the D-separation algorithm, first we check that under what conditions we have conditional independency in simple triples; then we're going to generalize these simple cases to more complex ones with bigger graphs and present a general algorithm named D-separation.
### Causal Chains First configuration is "causal chain".
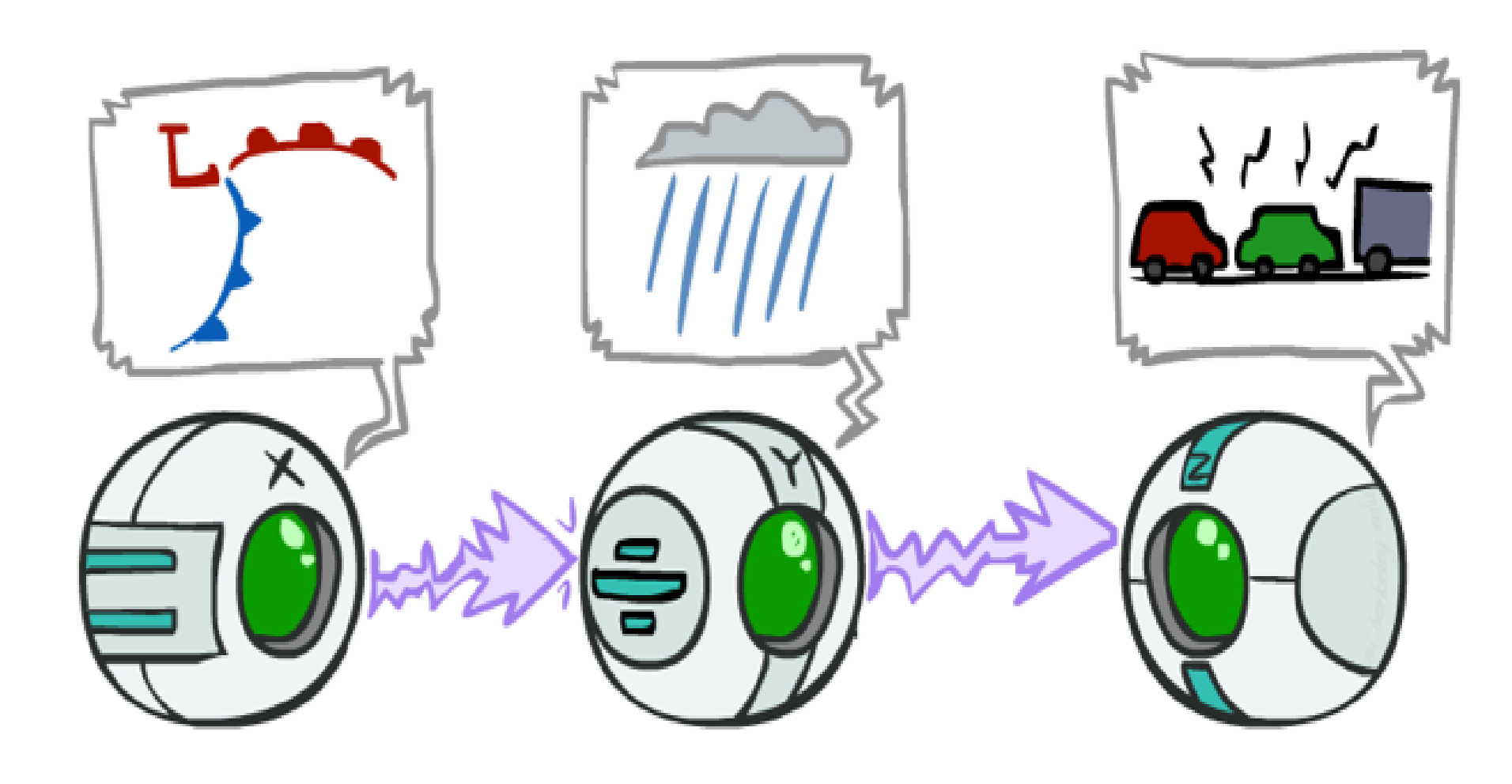
From left to right: X(Low Pressure), Y(Rain), Z(Traffic)
P(x, y, z) = P(x) P(y|x) P(z|y)Example:
Low pressure causes rain ( P( +y | +x ) = 1 ), high pressure causes no rain ( P( -y | -x ) = 1 ), rain causes traffic ( P( +z | +y ) = 1 ), no rain causes no traffic ( P( -z | -y ) = 1 ) and we suppose that having low pressure or high pressure is a random process so we have P(+x) = P(-x) = 0.5 .
Pay attention that in this example we have just one random process and the other two variables' values are deterministic according to causal chain.#### Is X guaranteed to be independent of Z ? The answer to this question is NO!
One example set of CPTs for which X is not independent of Z is sufficient to show this independence is not guaranteed.
So we need to compare P( Z | X ) vs P(Z) to figure out whether X and Z are independent or not. Then we suppose we have low pressure and traffic occured; meaning that we have +z for Z and +x for X. According to the definition of this example we know P( +z | +x ) = 1, but for P(+z) we should check if we have low pressure or high pressure. Knowing $$P(+z) = 0.5 \neq P(+z | +x)$$ we can conclude that X and Z are not independent.
#### Is X guaranteed to be independent of Z given Y? The answer to this question is YES!
We need to compare P( z | x, y ) vs P( z | y ) to figure out given Y, whether X and Z are independent or not. Proof:
$$P( z | x, y ) = \frac{P( x, y, z )}{P( x, y )} = \frac{P(x)P( y | x )P( z | y )}{P(x)P( y | x )} = P( z | y )$$
The above proof shows that in the triple causal chain, X and Z given Y are independent.
So we can say that information we know about Y as a central node blocks the influence of X on Z and for intuition about this statement, we can say that the only way in graph for X to get to Z passes Y. This is because Y and X and Z are not directly related. In other words while we have Y, X wouldn't add any information to our current knowledge for predicting Z.
### Common Cause Second configuration is "common cause".
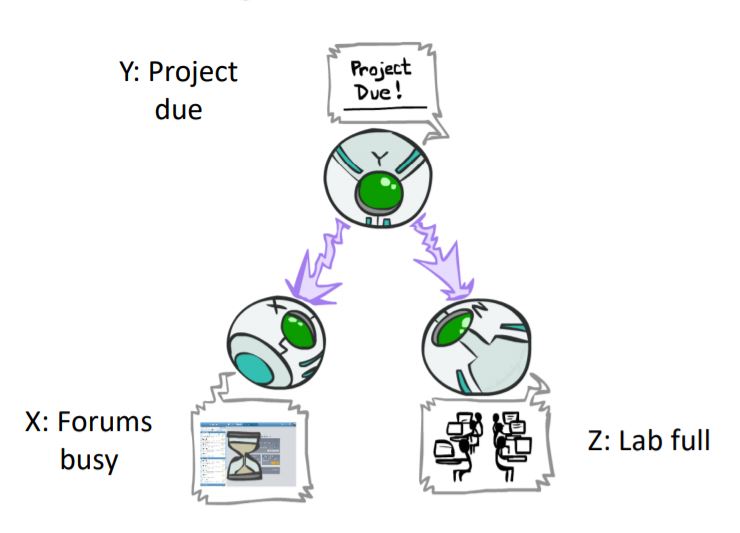
P(x, y, z) = P(y) P(x|y) P(z|y) Example:
Deadline for a project is near. This causes forums get busy ( P(+x|+y) = 1, P(-x|-y) = 1 ) and lab gets full ( P(+z|+y) = 1, P(-z|-y) = 1 ). We suppose that having near deadline or not is a stochastic process and divided equally. So, we have P(+y) = P(-y) = 0.5 .#### Is X guaranteed to be independent of Z ? 2 The answer to this question is NO!
One example set of CPTs for which X is not independent of Z is sufficient to show this independence is not guaranteed. So we need to compare P( Z | X ) vs P(Z) to figure out whether X and Z are independent or not. then we suppose that forums are busy and the lab is full; means that we have +z for Z and +x for X so according to definition of this example, we know that we should have P( +z | +x ) = 1; But for P(+z) we should check if we have a near deadline or not so P(+z) = 0.5; In conclusion this inequality proves that X and Z are not independent in general case.#### Is X guaranteed to be independent of Z given Y? 2 The answer to this question is YES!
So we need to compare P(z|x, y) vs P(z|y) to figure out with condition on Y are X and Z independent or not. Proof:
$$P( z | x, y ) = \frac{P( x, y, z )}{P( x, y )} = \frac{P(y)P( x | y )P( z | y )}{P(y)P( x | y )} = P( z | y )$$
the above proof shows that in triple common cause, with condition on Y, the X and Z are independent.
So in original case that we don't have any information about Y, knowledge about X lead us to conclusions about Y and then Z, though we wouldn't have independency; But in conditional form, having information about Y blocks the path between X and Z. Thus with knowing Y, X wouldn't add any information for predicting Z to our current knowledge.
### Common Effect Last configuration is "common effect" and sometimes called V-Structure.
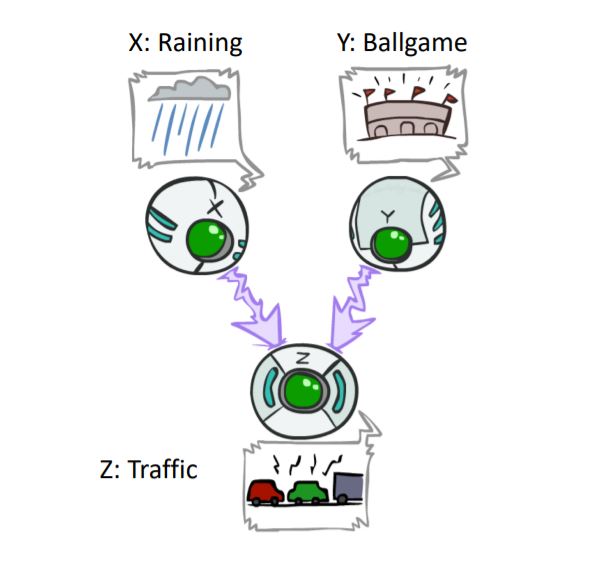
P(x, y, z) = P(x) P(y) P(z|x, y) In this structure, we have a phenomenon that has two different causes; for example both of raining and ballgame could cause traffic.
#### Are X and Y independent? The answer to this question is YES!
Although the ballgame and the rain cause traffic, but they are not correlated and with pure logic we understand it but still we need to prove this independency. Proof:
$$P(X, Y) = \sum_{z \in Z} P(X, Y, z) = \sum_{z \in Z} P(X)P(Y)P(z|X, Y) = P(X)P(Y) \sum_{z \in Z} P(z|X, Y) = P(X)P(Y)$$ So according to above proof and definition of independency, X and Y in this structure are independent.#### Are X and Y independent given Z? The answer to this question is NO!
Seeing traffic puts the rain and the ballgame in competition as explanation for occurance of traffic; it means that with seeing traffic, raining leads the possiblity of ballgame to lowest level and ballgame leads the possibility of raining to lowest level but this conclusion is just pure logic and for proving dependency, at least we need a counterexample.
Suppose P(+y) = P(+x) = 0.2 and P(-y) = P(-x) = 0.8. For occurance of traffic we have:- P(+z|+x, +y) = 0.95
- P(+z|+x, -y) = 0.9
- P(+z|-x, +y) = 0.9
P(+z|-x, -y) = 0.05
Now we can calculate P(+x|+z, +y) and P(+x|+z, -y) . For this purpose we should calculate P(+x, +z, +y), P(-x, +z, +y), P(+x, +z, -y) and P(-x, +z, -y). . Using Bayes' rule we have:
P(+x, +z, +y) = 0.038
- P(-x, +z, +y) = 0.144
- P(+x, +z, -y) = 0.144
P(-x, +z, -y) = 0.032
$$P(+x|+z, +y) = \frac{P(+x, +z, +y)}{P(+x, +z, +y) + P(-x, +z, +y)} = \frac{0.038}{0.182} = 0.209$$
$$P(+x|+z, -y) = \frac{P(+x, +z, -y)}{P(+x, +z, -y) + P(-x, +z, -y)} = \frac{0.144}{0.176} = 0.818$$
Since P(+x|+z, +y) and P(+x|+z, -y) aren't equal; given Z, X and Y aren't independent.
At last we can say that observing an effect activates influence between possible causes and this situation is backwards from the last two cases we studied.
### General Case Now with these three cases, we want to check that in any arbitary graph, what conditional independences can be found.
Usually in this case, having two random variables, the question is "given some other variables of that BN, are the two determined RVs independent or not?"
The procedure we use is analyzing the graph with those triples that we learned so far and trying to conclude independency of the determined RVs. What comes next is the steps to perform this procedure.#### Reachability First we shade the evidence nodes in the graph and then look for undirected paths between the two determined RVs that we want to check independency between them, in the resulting graph. The first rule is if two nodes are connected by an undirected path blocked by a shaded node, they are conditionally independent. This rule almost works everywhere except for V-structured paths where the bottom node is shaded.
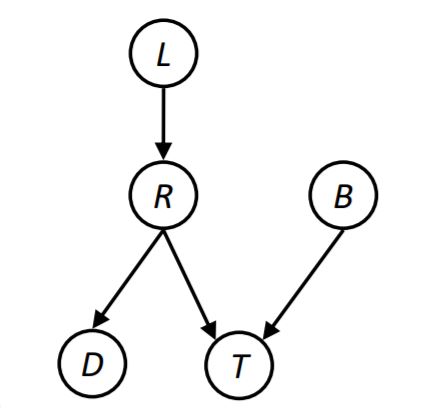
given R, L and B are conditionally independent
cause the path between them is blocked by R.#### Active / Inactive Paths Question: Are X and Y conditionally independent given evidence RVs (Z)?
Yes, if x and y are d-separated by z. Now we should define d-separation. d-separation means if we consider all undirected paths from X to Y after shading evidence variables, and none of these paths weren't active paths, we can say X and Y are d-separated by Z. but what is an active path? A path is active if each triple of it is active;Active Triples:
- Causal chain A → B → C where B is unobserved (either direction)
- Common cause A ← B → C where B is unobserved
Common effect (aka V-structure)
A → B ← C where B or one of its descendants is observedThe active and inactive triples are shown in the figure below.
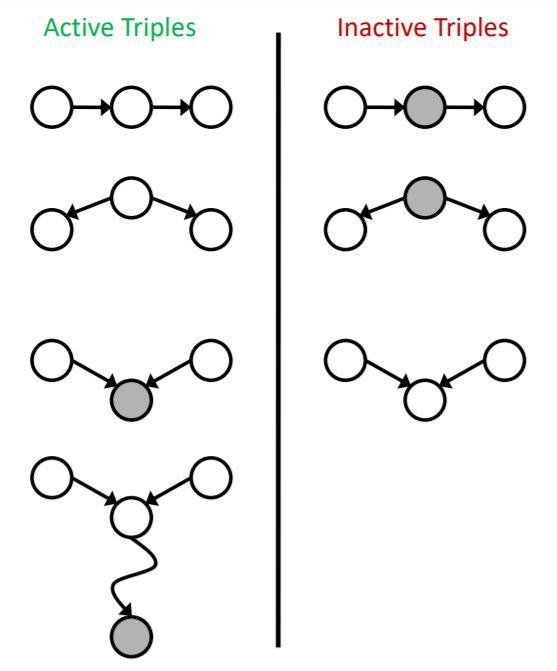
Notice that a single inactive triple makes a path inactive and for claiming independency between X and Y, we need all paths to be inactive.
If part of paths are inactive and part of them are active, neither we can say X and Y are independent nor we can say X and Y are dependant
but probably we can make an example for these cases that shows X and Y are dependent.
So in a nutshell, when we're given a query to determine conditionally independency of A and B given some evidence variables, we should check all paths between A and B:
If one or more paths were active, then independence isn't guaranteed.
If all paths were inactive, then independence is guaranteed.
#### Examples
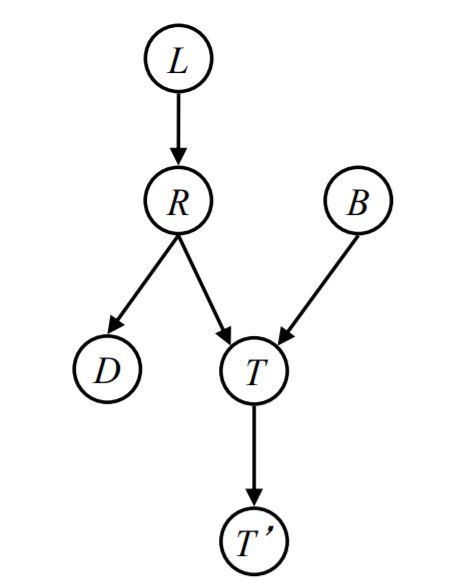
we want to check out conditionally independency between R and B with different evidences in the Bayes Net below.
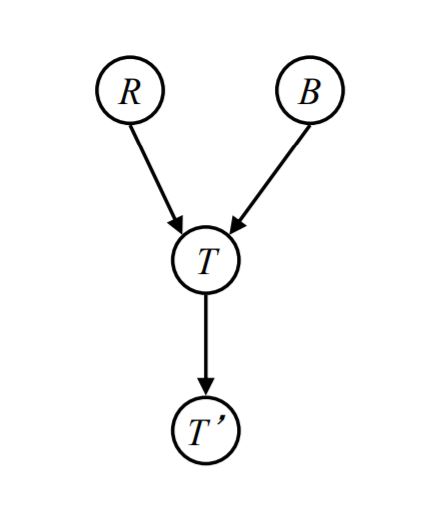
- without evidence: There is only one path between R and B and that's an inactive path according to third type of inactive triples which was shown already, so R and B are independent.
- evidence = T: According to third type of active triples which was shown already, the only path between R and B is active, so R and B aren't guaranteed to be independent.
- evidence = T': According to fourth type of active triples which was shown already, the only path between R and B is active, so R and B aren't guaranteed to be independent.
- independency between L and T', evidence = T: There is only one path between L and T' and that's an inactive path according to first type of inactive triples which was shown already, so L and T' are independent given T.
- independency between L and B, without evidence: There is only one path between L and B and that's an inactive path according to third type of inactive triples which was shown already, so L and B are independent.
- independency between L and B, evidence = T: According to third type of active triples which was shown already. The only path between L and B is active, so L and B aren't guaranteed to be independent given T.
- independency between L and B, evidence = T': According to fourth type of active triples which was shown already. The only path between L and B is active, so L and B aren't guaranteed to be independent given T'.
- independency between L and B, evidence = T, R: According to first type of inactive triples which was shown already. The only path between L and B is inactive, so L and B are independent given T and R.
We want to check out conditionally independency between T and D with different evidences in the Bayes Net below.
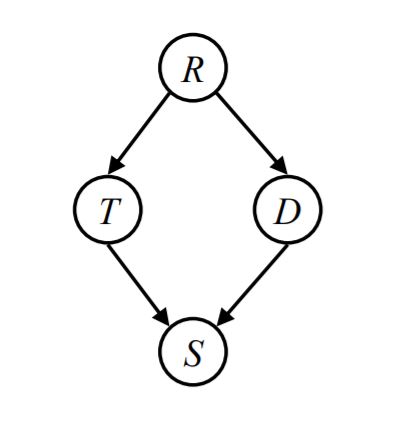
- without evidence: There are two paths between T and D and upper path is an active path according to second type of active triples which was shown already and lower path is an inactive path according to third type of inactive triples, so L and T aren't guarateed to be independent.
- evidence = R: Upper path is an inactive path according to second type of inactive triples which was shown already and lower path is an inactive path according to third type of inactive triples, so L and T are independent given R.
- evidence = R, S: Upper path is an inactive path according to second type of inactive triples which was shown already and lower path is an active path according to third type of active triples, so L and T are not guaranteed to be independent given R and S.
## Structure Implifications The important question that arises is that given Bayes' Net structure, can d-separation algorithm find all independent pairs for all possible evidence RVs?
The answer is NO! Actually, d-separation algorithm helps us conclude more conditional independences than before, but to get all of the conditional independences we should access all the CPTs or take some particular hypothesises on our Bayes' Net. The d-separation algorithm only helps us to get some of the conditional independences which are not obvious from bayes net definition.
D-separation's main concern is to find conditional independecies only from BN structure. While our structure might be overspecified, d-separation might fail to work at its best and miss a lot of conditional independences.
There are some structures that d-separation algorithm does a great job on and will find all of the conditional independences. Here are some examples:
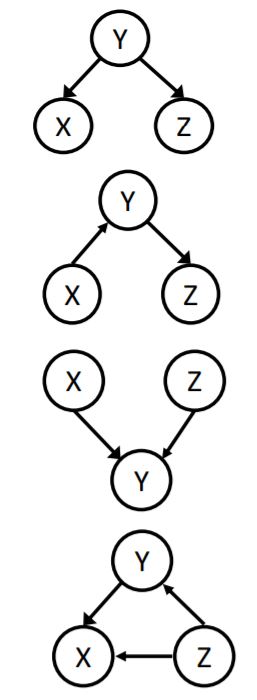
- For the first one, given Y, X and Z are conditionally independent. (Common Cause)
- For the second one, given Y, X and Z are conditionally independent. (Causal Chains)
- For the third one, X and Z are conditionally independent in general case. (Common Effect)
- For the last one, no conditional independency is concluded.
Topology limits distributions¶
These conditional independences enable us to group probabilistic models. There are 3 types of triple sets regarding to independency which is shown in the following figure:
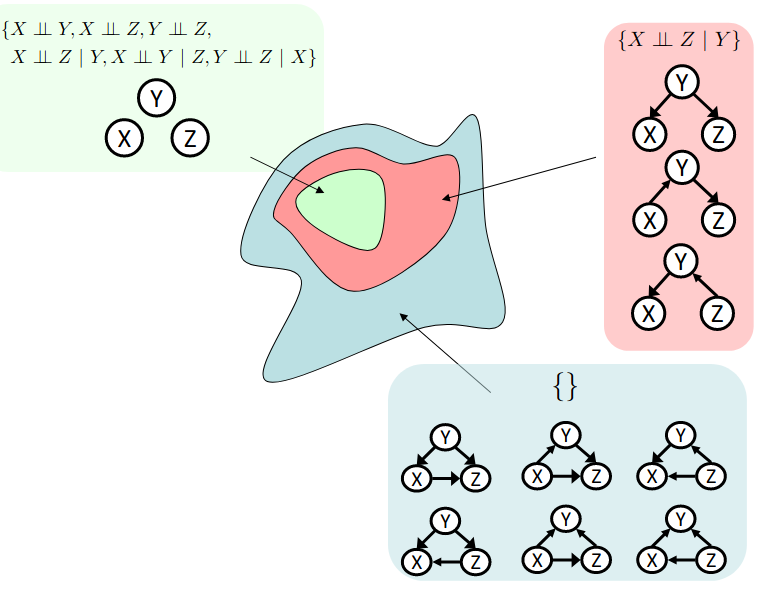
- Green colored independency triples in which every pair of RVs are independent of each other.(G)
- Red colored independency triples in which two RVs are independent given the 3rd one.(R)
- Blue colored independency tirples in which no independency is found.(B)
The following relation holds: $$G \subset R \subset B$$
Summary¶
Bayes' Net is a directed acyclic graph that compactly encodes joint distribution and there are guaranteed independences of distrubutions that can be deduced from it. D-separation is a method to exploit these guaranteed independences from Bayes' Net, but exploiting all possible independences needs precise calculations using CPTs or particular assumtions of RVs.